Editorial
Vanna-Volga and the Greeks
Many people ask us what’s so special about calculating Greeks in the vanna-volga approach. Isn’t it like calculating bumped values and ratios of differences?
On the other hand, did you ever wonder, why for instance a professional system like SuperDerivatives doesn’t provide vanna-volga Greeks along with its “market price”, which is known to be based on vanna-volga and other adjustments?
Figure 1: Difference of vanna-volga based KO call option value and its corresponding vanilla option value, strike on the x-axis
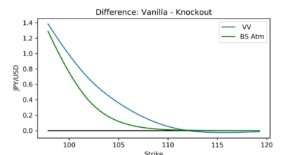
For exotics, we like to see prices consistent with vanilla options. A simple example is a barrier option, say a down-and-out call in USD-JPY with barrier 102, spot 109.24. When we move the barrier away, we want to observe a monotone convergence of the barrier option price to the vanilla option price. In particular, the barrier option price should never exceed the vanilla option price. Figure 1 shows the difference of the vanilla and the regular knock-out option value for varying strikes. In a Black-Scholes model with constant volatility the barrier option value is always below the vanilla option value.
Surprisingly we observe that in the vanna-volga approach the knockout option value can be slightly higher than the vanilla option value, so the difference of a vanilla minus knockout option value can become negative, see the blue curve in Figure 1. Analyzing this, it turns out that we are in a situation where for the vanilla option value the vanna-volga hedging costs are negative or, more generally, where the sum of the vanna and the volga term in the vanna-volga formula is negative and the vanna-volga value is below the flat volatility Black-Scholes value.
For knockout options the vanna and the volga term are usually multiplied with some factor smaller than one (often a function of the no-touch probability of the barrier) and the correction term to the Black-Scholes value is negative, but not negative enough anymore to cause a knock-out option value above the vanilla option value.
To force minimum consistency one can at the very least cap the barrier option value at the vanilla option value or floor their difference at zero, see Figure 2.
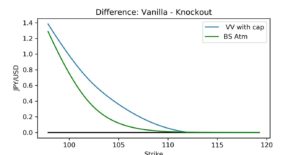
Figure 2: Difference of vanna-volga based KO call option value and its corresponding vanilla option value, floored at zero, strike on the x-axis
Implementing such a consistency rule is quite easy, but we now lose smoothness of the value function. And as we know this may cause jumps and spikes in the Greeks, especially when we compute derivatives by finite differences, i.e. bumping market data.
Figure 3 shows the vega profile for varying strikes for the above example computed by bumping volatility by an absolute value of 0.1%.
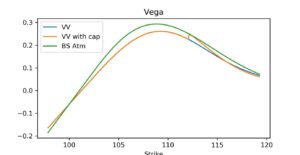
Figure 3: Vega on the strike space of a regular knock-out call, comparing vanna-volga approach with and without consistency rule (cap)
Figure 4 shows the gamma profile for varying strikes for the above example computed by bumping spot by an absolute value of 0.01.
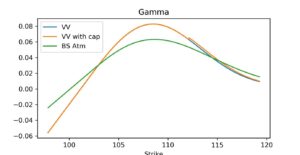
Figure 4: Gamma on the strike space of a regular knock-out call, comparing vanna-volga approach with and without consistency rule (cap)
In this example the kinks and jumps we see in the graphs are unpleasant, but not dramatic. The problem is that the kinks occur at parameter levels that are not easy to predict – in contrast to non-smooth behavior at a barrier level, which is known in advance and allows us to compute one-sided finite differences or shift the barrier.
Non-smooth value functions at non-predictable locations of kinks in combination with parameter bumping can now really lead to exploding Greeks, as can be seen in Figure 5. Just by selecting other strikes we hit a region where gamma takes an arbitrary value.
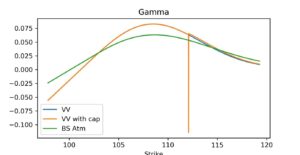
Figure 5: Exploding gamma on a different strike grid of a regular knock-out call, cause by a vanna-volga approach with consistency rule
Of course, one can try to model smoother transition rules between the curves for each consistency rule, but this will lead to an endless patchwork.
The situation becomes even worse, if we value vanilla options from an already constructed smile surface. Then the vanilla options are valued correctly, but one would need to add many more rules to avoid inconsistencies caused by valuation based on the smile and valuation based on the vanna-volga approach[1].
Valuing first generation exotics with the vanna-volga approach approximated their prices well in past and still yields very fast and simple rough indicative prices for touch contracts in FX markets. However, computing vanna-volga Greeks was and remains complicated. This is caused by having to impose many consistency rules to a seemingly simple vanna-volga formula.
Today we discussed only some of the technical difficulties and traps but didn’t even explore if the Greeks computed in vanna-volga are useful and correct quantities for risk management.
Overall, we learn that if we impose conditions to make pricing of exotics in vanna-volga approaches consistent with vanilla options, we obtain instable Greeks. Without consistency conditions, the Greeks might be smoother, but the values may lead to arbitrage. It will require a lot of patchwork to cure all the headaches at one go.
Consequently, we consider it rather worth investing the time to compute stable Greeks within consistent models, knowing that there are still enough numerical challenges left. And with the model class of SLV and its variants we have models at hand, that are flexible enough to fit the prices in many FX option markets.
[1] Recall MathFinance Newsletter 352 of 28 May 2019, https://www.mathfinance.com/newsletter-352/
Andreas Weber and Uwe Wystup
MathFinance AG
————————————————————————————————————————————-
Upcoming Events
MathFinance Conference 2020
1-2 September, 2020
Marriott Hotel, Canary Wharf, London
In view of the uncertainty caused by the Coronavirus outbreak, MathFinance has decided to postpone its 20th annual MathFinance Finance conference to 1st and 2nd September to guarantee a safe and successful participation. The location remains unchanged. A majority of speakers have confirmed their attendance and the full agenda will be uploaded in due course.
For more information please visit:
https://www.mathfinance.com/events/mathfinance-conference-2020/
————————————————————————————————————————————-
MathFinance Trainings
MathFinance is excited to host its new training offerings for 2020. Throughout out the year we will be uploading new courses that will be offered at our new offices in Kaiserstrasse 50, Frankfurt am Main. In addition to the FX options course being taught by Dr. Uwe Wystup, we are currently offering three brand new courses on:
i) Interest Rate Derivatives – Hedging and Managing Risk
ii) An introduction to Equity Derivatives
iii) Machine Learning & Artificial Intelligence Applications for Financial Markets
The first two courses will be taught by Rubin Rajendram, who is an international expert on exotic derivative trading, pricing, analytics and risk management and is a frequent speaker at international conferences.
The third course is taught by Dr. Thorsten Schimdt, who is currently a senior financial engineer at MathFinance and is an expert in financial and actuarial modelling, statistics and machine learning. Thorsten also is a professor for mathematical stochastics at University of Freiburg
For further details on our offerings please visit:
https://www.mathfinance.com/trainings/
————————————————————————————————————————————-
Treasury Bootcamp – organized by ASTC, Dubai
Barcelona, 6-10 April, 2020
COURSE OVERVIEW
This 5-Days intensive “Treasury Boot Camp “program designed especially for banking, investment companies and other financial institutions treasury professionals enriched with treasury best practices, FX, MM, Dealing, Derivatives, ALM, best models and techniques used and latest technology. You will also have the opportunity to meet fellow professionals from around the world and build relationships, exchange information and develop a great network that will support you in your on-going treasury career, sharing the knowledge and learn the best techniques.
WHO SHOULD ATTEND?
- Treasury managers
- Back and Middle Office operations
- ALM and investment Companies
- FX and Money Market professionals
- Auditors and Compliance Officers
- Risk managers, Finance Directors and Analysts
To know more about the course content and expert trainer, please click on this link.
MathFinance newsletter subscribers will receive a discount of USD 200 on this course plus other applicable discounts.
For additional enquiries please get in touch with:
Ali Danish | Director Training and Development
T +971 4 2211141 | M +971 52 8488764 E danish@astcdubai.com |
————————————————————————————————————————————-
Machine Learning for Option Pricing, Calibration and Hedging
with Jörg Kienitz and Nikolai Nowaczyk
July 2-3rd, 2020
London
Cost: £1999
‘Early Bird’ Discount – 10% before 15 April, 2020
The goal of this two-day workshop is to provide a detailed overview of machine learning techniques applied for finance. We offer insights into the latest techniques of using such techniques for modelling financial markets where we focus on pricing and calibration.
We not only tackle the theory but give practical guidance and live demonstrations of the computational methods involved. After introducing the subject we cover Gaussian Process Regression and Artificial Neural Networks and show how such methods can be applied to solve option pricing problems, speed up the calculation of xVAs or apply them for hedging.
We further show how to use existing pricing libraries to interact with machine learning environments often set up in Python.
We explain how to set up the methods mainly in Python using Keras, Tensorflow or SciKit Learn. We give many examples which are directly related to financial mathematics and can be explored further after the course. All the material is available as Jupyther notebooks. For Gaussian Processes we use Matlab and Python examples.
This workshop covers the fundamentals and it illustrates the application of state-of-the-art machine learning applications for application to Mathematical Finance.
Further information, brochure and registration: http://bit.ly/ml-for-finance
————————————————————————————————————————————-
Digital Finance
Call for Papers
Special Issue on Artificial Intelligence, Machine Learning and Platform Innovation in Quantitative Finance (MathFinance Conference 2020)
Overview
Traditionally, Quantitative Finance has revolved around the development of parsimonious models that yield some economic understanding of financial markets. In recent years, there has been a change in this paradigm by embracing data-driven methods from AI and ML. Here are some reasons that explain this shift: greater amounts of financial data are available that require fast processing; financial analysis and computations are supplemented by non-financial data, such as textual data, in order to create new insights; data-driven methods allow to detect trends and market changes that would not be observed with a rigid model. At the same time, platform technology has taken over trading of spot and derivatives in financial markets. Pricing models, Greeks and risk calculation have to be faster and more accurate than ever before. The special issue welcomes contributions that explore innovative uses of AI / ML methods and platform technology in Quantitative Finance. These can involve economic, quantitative, computational and technological aspects.
Speakers and participants of the MathFinance Conference 2020 are encouraged to submit their work, but the special issue also welcomes contributions from the community.
Editors of the Special Issue
Prof. Dr. Natalie Packham, Berlin School of Economics and Law
Prof. Dr. Uwe Wystup, Managing Director, MathFinance
Instructions for Submission
For submission, authors are requested to access the access the Editorial Manager at the following URL: http://www.editorialmanager.com/dfin/default.aspx. Please answer ”Yes” when asked if your manuscript belongs to a special issue and select the special issue in the list that will pop up.
Potential authors are reminded that all papers that are finally accepted for this special issue will be subject to format restrictions complying with the publisher’s standards. To speed up publication, and to ensure a unified layout throughout the special issue, authors are kindly advised to use LaTeX. Springer’s LaTeX template (click here) can be used to prepare source files (please choose the formatting option “smallextended”). The authors are highly recommended not to modify the class file by introducing personal settings and/or definitions.
Important Dates
Deadline for paper submission: 30 April
First-round decisions: 31 May
Deadline for second-round submission: 15 July
Final decisions: 31 August
About Digital Finance
The journal is a top tier peer-reviewed academic and practitioner journal that publishes high-quality articles with a focus on digital finance and innovation as well as on the analysis of digital and internet innovations on financial services and the economy. The journal publishes theoretical or empirical, qualitative or quantitative papers of interest to academics, practitioners, and regulators with the emphasis on empirical, financial market, and investment innovation, financial policy research and recommendations related to improving the welfare in the digital economy. Further details on this journal are available on the Springer website: https://www.springer.com/42521
