Editorial
Long Call Option with Negative Time Value
In general derivatives textbooks the value of a call option is often presented as the sum of the intrinsic value max(0,ST-K) and the time value as illustrated in Figure1. As usual, I denote by STthe spot price at maturity T and by K the strike price.
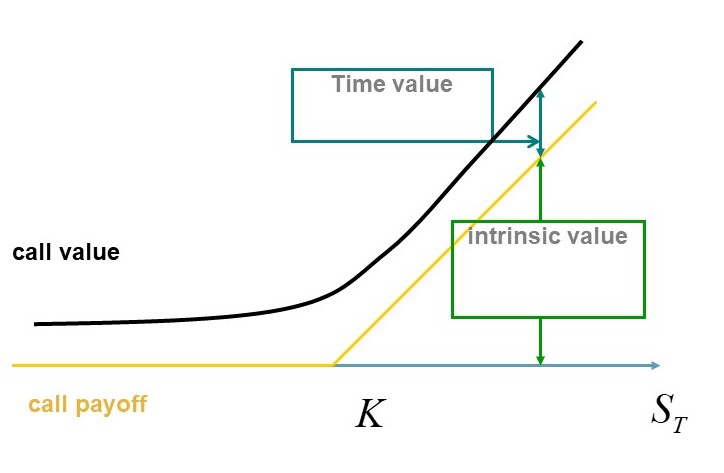
Figure 1: payoff and value function of a call option
One question I like to ask is if the time value can ever be negative. Since most of the time I get “no” as an answer, with the additional reasoning that otherwise the holder of the call option would exercise earlier, let me clarify today: In FX context options are normally of European exercise style, which means that the holder can only exercise them on the maturity date. American options that allow exercise during the live time as well are more common in equities.
The best way to understand the reason is to consider FX options in their traditional way as hedging instruments for corporate treasurers. A corporate treasurer would normally not buy an American option, because (a) it would be unnecessarily expensive compared to the same European option and (b) the cash flow to be hedged is normally not available before maturity. Consequently, unless you say otherwise, FX options are of European exercise style.
That clarified, how can a European call option have a negative time value? We can recycle our knowledge about American options and argue that the American option would only be exercised early if the foreign interest rate is significantly larger than the foreign interest rate. For the equity options fans this is equivalent to a call on a dividend paying stock. A real-live example is a 1Y USD call JPY put, which I have priced in Eikon, see Figure 2.
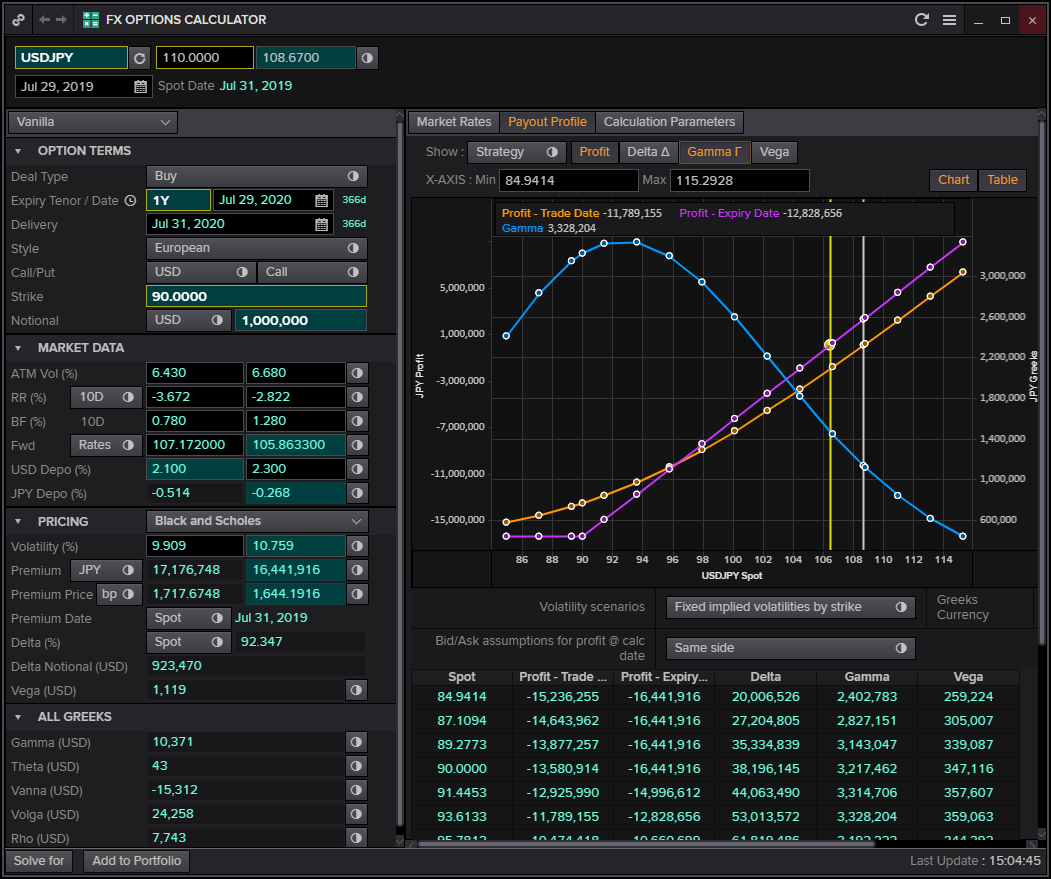
Figure 2: USD/JPY 1Y USD call priced in Eikon’s FX Option Calculator
With spot at 110, strike at 90, the intrinsic value is 20 JPY per USD, so 20M JPY on a notional of 1M USD. Not being able to exercise early means losing the USD interest rate of 2.10%, so the price of the USD call is lower than this intrinsic value. It is shown as about 17M JPY in Eikon (although it is interesting that the bid price seems higher than the offer price, food for thought). The graph shows in fact that the value function crosses the intrinsic value (=payoff) if the option is deep enough in the money (ITM).
For the Greeks, we spot that the USD call option is long gamma (as any long vanilla option is long gamma), see the blue curve in Figure 2. This option is also long theta in the deep ITM region. Thus, the trader with this option in his book will make money by delta hedging it and at the same time make money as time passes. Where is the catch?
This is not an Eikon bug: a negative time value implies a long theta position, because the value function will have to converge to the payoff, so the ITM part of the value function will increase towards the payoff as time passes. The catch is that the deep ITM call is very similar to a long USD/JPY forward contract, whose dominating risks are the change of spot and carry, the difference between the USD and the JPY interest rate.
As a general summary: any FOR call DOM put option with a backwardation in the FOR/DOM forward curve will show this feature of a negative time value, be long theta and long gamma. Some derivatives textbooks or common misconceptions need to be updated.
Uwe Wystup
Managing Director of MathFinance
Upcoming Events
FX Exotic Options in Frankfurt 2019
December 16 – 18, 2019
Lecturer: Prof. Dr. Uwe Wystup
This advanced practical three-day course covers the pricing, hedging and application of FX exotics for use in trading, risk management, financial engineering and structured products.
FX exotics are becoming increasingly commonplace in today’s capital markets. The objective of this workshop is to develop a solid understanding of the current exotic currency derivatives used in international treasury management. This will give participants the mathematical and practical background necessary to deal with all the products on the market.
Check the details
Register either directly here or use the single registration pdf or the group registration pdf
