Editorial
Can you replicate a call option with two European digital options?
A European digital pays one unit of currency (domestic or foreign) at a predefined expiry date, if on that date the observed FX spot fixes above a predefined strike level. Can you statically replicate a call option with two European digital options?
The question may seem rather elementary but, asking it at quant candidates during technical interviews, I was surprised by the small number of correct answers. In fact, most readers will probably be more familiar with the inverse question: “can you statically replicate a European digital option with call options?”
The latter can be answered by taking the limit of a call spread when the two strikes are converging to each other (and to the strike of the European digital). This is a typical trader’s approach to the risk-management of digitals.
Coming back to our original question, suppose that you own a EURGBP call option with a maturity of 1Y and a strike of 0.85 (GPB per EUR). Now let me simply describe the cash flows at maturity in plain English:
At maturity, if the EURGBP spot fixes above 0.85, you exercise your call option:
- You pay 0.85 (=strike K) GBP.
- You receive 1 EUR.
These two legs correspond respectively to
- A SHORT domestic European digital with strike K and notional K
- A LONG foreign European digital with strike K and notional 1.
The call option is thus exactly replicated by the difference between two digitals, one paying K units of domestic currency (=cash-or-nothing), and one paying 1 unit of foreign currency (=asset-or-nothing), if the spot fixes above the strike.
Describing the call payoff in mathematical terms, the decomposition is straightforward:
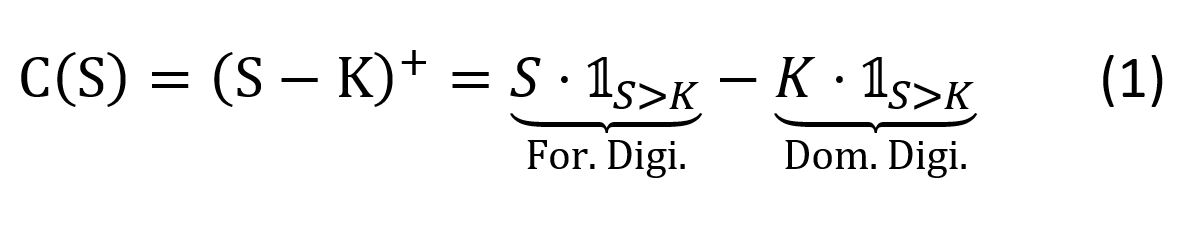
The factor S in the first term comes from the conversion of the foreign digital payoff (in EUR) into domestic currency GBP. Equation (1) is graphically represented in Figure 1.
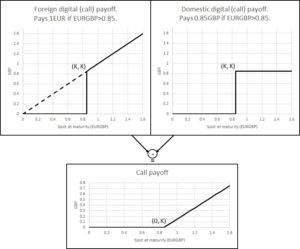
Figure 1: geometric decomposition of the call payoff into a domestic and a foreign digital.
Note that so far, we haven’t made any model assumption. This is a static replication which holds just by payoff construction. Let us stress that this replication also holds for the Greeks, not only for the price.
Expressing the (undiscounted) call price under the Black model, one immediately recognizes the same replication pattern:
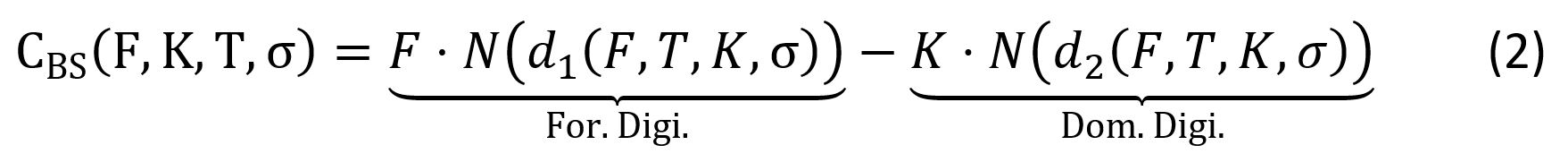
Where N(d1) and N(d2) represent respectively the probability of being “In-The-Money” (S>K) at time T under a foreign (EUR) and a domestic (GBP) risk-neutral measure.
As an independent verification, Figure 2 presents results obtained with SuperDerivatives, pricing our EURGBP example. We put together a small portfolio containing a long position in the EURGBP Call (column1), and a short position in its static replication with Digitals (columns 2 and 3), so that the net total position should be exactly zero.
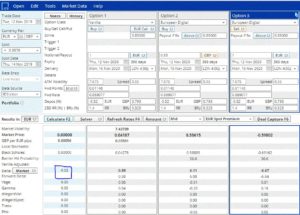
Figure 2: pricing a (Long) EURGBP call and its (Short) static replication in SuperDerivatives.
As expected, the (mid) price of the portfolio is almost exactly zero (to some minimal numerical noise). This is also the case for the Greeks, except for Delta where we observe a small – yet material- difference of 3% between the call (D=59%) and its static replication (D =56%). This example shows that, despite the apparent simplicity of the approach, it is relevant as soon as you deviate from the plain constant-vol Black-Scholes mode. In the present example, the small Delta difference could come from slight numerical differences in the way the volatility smile is incorporated in foreign and domestic Digitals.
Whether you are a model developer, a model user or a validator, this kind of replication very often comes in handy, and should be used without moderation for testing purpose, or for extending the scope of products in your library.
Let me finally mention that simple extensions are possible be adding common exotic features to the European Call and Digitals. For example, a Call with American barrier(s) will be similarly replicated with domestic and foreign Digitals sharing the same American barrier(s).
Dr. Frédéric Bossens
Director, Senior Quant
Upcoming Events
MathFinance Conference 2020
30th &31st March 2020
Marriott Hotel, Canary Wharf, London
MathFinance hosts the annual Conference in Frankfurt which is tailored to the quantitative finance community. For 2020 and it’s 20th year running, we are moving our Conference to London. Providing cutting-edge research and brand new practical applications, the conference is intended for practitioners in the areas of trading, quantitative or derivative research, risk and asset management, insurance as well as for academics studying or researching in the field of financial mathematics.
This year the theme of the first day of the conference lies around Artificial Intelligence and Machine Learning in the field of Quantitative Finance. The second day will focus on quantitative finance subjects with a specific focus on FX Derivatives. This year we are especially pleased to welcome Dr. Bruno Dupire, who is best known for his contributions to local volatility modelling and Functional Ito Calculus , Dr. Jesper Andreasen aka “ Kwant Daddy” who received the Risk Magazine’s Quant of the Year award in 2001 alongside other distinguished speakers from the world of finance and academics.
As always, we expect around 100 delegates both from the academia and the industry. This ensures a unique networking opportunity which should not be missed. A blend of world renowned speakers ensure that a variety of topics and issues of immediate importance are covered.
This event is a must for everyone in the quantitative financial industry.
Further details
Introduction to QuantLib Development with Luigi Ballabio
In partnership with www.moneyscience.com
March 23-26, 2020 – London
Mathfinance Newsletter Subscribers – 10% Discount with code MFIN20
The goal of this three-day intensive hands-on course is to take a birds-eye look at the design of theQuantLib library as well as its rationale, to examine its implementation, and thus to learn how one’s own code can be fitted on top of QuantLib to reuse and benefit from provided functionality. The course will focus on QuantLib proper, i.e., on the C++ library and won’t cover extensions such as the Excel addin.
What do you learn?
- The overall design of the QuantLib library
- The rationale of its design and implementation
- The correct use of the main classes in the library
- The design and use of some of its framework, such as the tree and Monte Carlo frameworks
About the Speaker
Luigi Ballabio is senior quantitative developer at StatPro Italia srl, part of StatPro Ltd. He’s one of the founders, administrators and lead developers of the QuantLib project. He holds a Ph.D. In Applied Nuclear Physics from the University of Uppsala.
Further Information: http://bit.ly/quantlib2020
Pricing FX derivatives: Stochastic Local Volatility and Mixture Local Volatility Models
Cass Business School
Dec 4, 2019
Dr Frédéric Bossens, director at MathFinance will give a talk at Cass Business School on Dec 4 18:10 on the subject
Open Positions
Tenure Track Faculty in Mathematical Finance or Optimization at Carnegie Mellon University
The Department of Mathematical Sciences at Carnegie Mellon University invites applications for a tenure-track faculty position, to begin September 1, 2020. The position is in mathematical finance or optimization, and the rank is open.
Preference will be given to candidates who have shown outstanding promise and/or excellent accomplishments in research, and are pursuing a vigorous research program including major contributions beyond the doctoral dissertation. Promise of excellent ability to teach and mentor students of diverse backgrounds is a plus.
The Department has long-standing strength in mathematical finance and plays a central role in Carnegie Mellon’s interdisciplinary masters and bachelors degree programs in computational finance. The Department also has a popular undergraduate degree concentration in Operations Research, and interest in graduate level courses in optimization is growing. Candidates for this position are expected to be able to contribute to one or more of these educational programs.
Applications should be submitted by October 31, 2019 for full consideration.
The Department of Mathematical Sciences is committed to increasing the diversity of our faculty. Carnegie Mellon considers applicants for employment without regard to, and does not discriminate on the basis of, gender, race, protected veteran status, disability, sexual orientation, gender identity, and any additional legally protected status.
Applicants should submit materials electronically at www.mathjobs.org and https://apply.interfolio.com/69158. This includes a cover letter, curriculum vita, list of publications, a statement describing research interests, and at least three letters of recommendation (including at least one that specifically addresses teaching). Letters of recommendation will be solicited through mathjobs only. Recommenders who are unable to submit their letters electronically may mail them to: Tenure Track Search Committee, Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213.
Applications may be accepted and reviewed until any open positions are filled.
=====================================================================
Post Doctoral Appointments in stochastic analysis/financial mathematics at Carnegie Mellon University
The Department of Mathematical Sciences plans to make multiple two-or three-year post-doctoral appointments in stochastic analysis, with at least one appointment being in financial mathematics, beginning in September 2020.
Preference will be given to candidates who have shown outstanding promise and/or excellent accomplishments in research. A PhD in mathematics or a closely related discipline is required.
The Department of Mathematical Sciences is committed to increasing the diversity of our faculty. Carnegie Mellon considers applicants for employment without regard to, and does not discriminate on the basis of, gender, race, protected veteran status, disability, sexual orientation, gender identity, and any additional legally protected status.
Applicants should submit all materials electronically through mathjobs and https://apply.interfolio.com/69829. This includes a curriculum vita, a list of publications, a statement describing current and planned research, and at least three letters of recommendation (including at least one that specifically addresses teaching). Letters of recommendation will be solicited through mathjobs only. Recommenders who are unable to submit their letters electronically may mail them to: Stochastic Analysis Postdoc Search, Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213.
For full consideration, applications should be submitted by December 2, 2019. Applications may be accepted and reviewed until any available positions are filled.
