Editorial
Reverse-Knock-Out Pricing Case Study:
Stochastic Local Volatility vs. Vanna-Volga
Today, let’s revisit pricing a reverse knock-out option (RKO). This call or put option knocks out if at any time between trading time and the expiry date the spot hits or crosses a pre-specified barrier. For the RKO, the barrier is in the money, i.e. above the strike for a call, and below the strike for a put. With the barrier in the money, this option creates a large intrinsic value if the spot is near the barrier. This product is a popular building block in FX structured forwards for corporate treasurers, and also as part of Dual Currency Investments in the private banking industry. The buy-side would normally not trade stand-alone RKOs, unless they are hedge-funds deriving their adrenaline level from model arbitrage.
We consider a GBP put CHF call, strike 1.3708, down and out at 1.1389, expiring in 190 days on 8 Nov 2019, delivery date 10 Nov 2019, whose payoff is illustrated in Figure1.
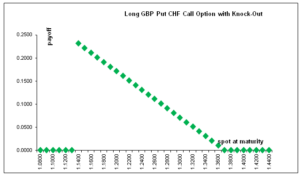 Figure 1: Down-and-out GBP put CHF call
Figure 1: Down-and-out GBP put CHF call
We use the following market data on horizon 2 May 2019: spot reference 1.3309, 6M GBP deposit rate 0.7456%, CHF deposit rate -0.9155%, forward 1.3197, 9M GBP deposit rate 0.7648%, CHF deposit rate -0.948%, forward 1.3136, 6M ATM volatility 7.233%, 9M ATM volatility 7.385%. The volatility smile in Figure 2 shows a significant down skew (negative risk reversals) and also illustrates that the Heston model does not fit the input perfectly, as it is a parametric model with limited number of possible shapes, whereas the stochastic-local-volatility (SLV) models fit the smile well, as their local volatility component always makes sure the vanilla market is well represented.
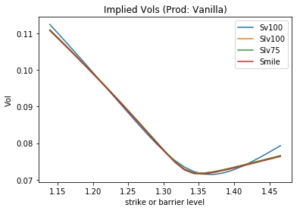 Figure 2: GBP/CHF volatility smile on the strike space. Smile refers to the MathFinance fit, Sv100 is the best possible fit in the Heston model, Slv100 is a stochastic-local volatility model with 100% stochastic mixing factor, Slv75 the corresponding one with 75% mixing factor.
Figure 2: GBP/CHF volatility smile on the strike space. Smile refers to the MathFinance fit, Sv100 is the best possible fit in the Heston model, Slv100 is a stochastic-local volatility model with 100% stochastic mixing factor, Slv75 the corresponding one with 75% mixing factor.
Fitting the volatility smile gets worse if we try to use vanna-volga, see Figure 3. The vanna-volga fit does not naturally fit the smile at points other than ATM and 25-delta strikes. Consequently, when pricing and RKO with a barrier far away, in a vanna-volga approach, the price does not converge to the corresponding vanilla option price. This is a major drawback of vanna-volga: exotics are priced inconsistent with the vanilla options market. Additionally, we observe that even the way we design a vanna-volga model can lead to different smile curves (and hence to different exotics prices). Vv takes into account the cost of vanna when hedged with a risk reversal, and the cost of volga when hedged with a butterfly[1], whereas Vv2 takes into account the cost of vega, vanna and volga jointly hedged with three vanilla options.
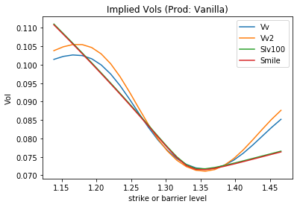 Figure 3: GBP/CHF volatility smile on the strike space. The two versions of vanna-volga Vv and Vv2 fit the smile only at the money and for 25-delta strikes.
Figure 3: GBP/CHF volatility smile on the strike space. The two versions of vanna-volga Vv and Vv2 fit the smile only at the money and for 25-delta strikes.
Next let us turn to the pricing of the RKO in various models. Figure 4 shows that all the local- and stochastic and their mixture models lead to price deviations from TV (theoretical value = Black-Scholes model price using ATM volatility). Deviations converge to zero as the barrier converges to the current spot (right-hand side), when all prices are zero in all models. If the barrier moves far away from current spot (left-hand side), the RKO prices should converge to the corresponding vanilla prices (which they do except for the vanna-volga approaches).
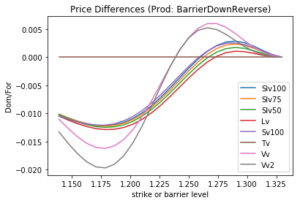 Figure 4: Differences to TV (theoretical value) of the GBP put CHF call RKO for a variety of models, measured in domestic currency per one unit of foreign currency notional. “Lv” represents a pure local volatility model. The barrier is moving so different option prices are calculated.
Figure 4: Differences to TV (theoretical value) of the GBP put CHF call RKO for a variety of models, measured in domestic currency per one unit of foreign currency notional. “Lv” represents a pure local volatility model. The barrier is moving so different option prices are calculated.
While the vanna-volga approaches still exhibit a broadly similar pattern, they still fall outside the typical range of local volatility and stochastic volatility pricing. Conclusion: vanna-volga based RKO pricing is at the most suitable for valuations for accounting and reporting purposes. For market makers, the prices are too far outside the SLV market standard, independent of the mixing factor.
The markdown of 50-100 pips is significant. We illustrate now where it comes from. Recall that an RKO Put with strike K and barrier B can be statically replicated by a regular KO Call with strike K, a short strike-out call at B, and a no-touch at B with notional of the maximum intrinsic value K-B. We observe from Figure 5 that most the markdown is caused by the touch contract. If the price of the No-Touch is marked down, the price of the RKO is marked down, too.
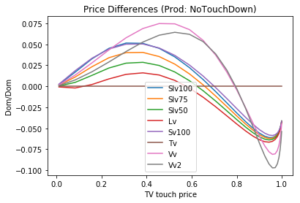 Figure 5: One-Touch mustache: differences to TV (theoretical value) of the CHF-paying No-Touch for a variety of models, measured in domestic currency per one unit of domestic currency notional. The lower barrier is moving so different option prices are calculated.
Figure 5: One-Touch mustache: differences to TV (theoretical value) of the CHF-paying No-Touch for a variety of models, measured in domestic currency per one unit of domestic currency notional. The lower barrier is moving so different option prices are calculated.
For the sake of completeness we illustrate the model impact for the RKO GBP call CHF put in Figure 6.
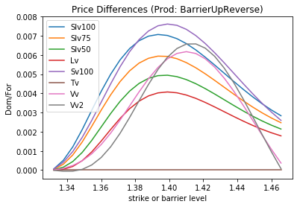 Figure 6: Differences to TV (theoretical value) of the GBP call CHF put RKO for a variety of models, measured in domestic currency per one unit of foreign currency notional.
Figure 6: Differences to TV (theoretical value) of the GBP call CHF put RKO for a variety of models, measured in domestic currency per one unit of foreign currency notional.
Which of the mixing factors represents the market of traded RKO options can be determined by sliding the mustache between Lv (mixing factor 0%) and Slv100 (mixing factor 100%), so that most observable RKO prices are met. This way one could arrive at Slv75 or Slv50. Note that all RKOs are priced without any face-lifting.
The overall conclusion is that a sound application of SLV models leads to consistent pricing of exotics and vanilla options across the product and parameter range, a frequent requirement of model governance, – and a goal that vanna-volga based approaches will have a hard time fulfilling.
Uwe Wystup
Managing Director of MathFinance
[1]https://www.slideshare.net/wystup/fxmodels-slidesenglpublic
Upcoming Events
FX Exotic Options in Frankfurt 2019
September 18 – 20, 2019
Lecturer: Prof. Dr. Uwe Wystup
This advanced practical three-day course covers the pricing, hedging and application of FX exotics for use in trading, risk management, financial engineering and structured products.
FX exotics are becoming increasingly commonplace in today’s capital markets. The objective of this workshop is to develop a solid understanding of the current exotic currency derivatives used in international treasury management. This will give participants the mathematical and practical background necessary to deal with all the products on the market.
Check the details
ARPM Bootcamp
August 12 – 17, 2019, New York
The Advanced Risk and Portfolio Management (ARPM) Bootcamp is the most intense 6-day training in data science for finance, quantitative risk modeling and portfolio construction.
Taught August 12-17 by Dr. Attilio Meucci, the ARPM Bootcamp has hundreds of onsite attendees, practitioners and academics.
Learn in a 50-hour Program the most advanced quantitative techniques in data science and machine learning, algorithmic trading, market modeling, factor modeling, investment risk management, liquidity modeling, portfolio construction, and much more.
Practice in the ARPM Lab with theory, case studies, data animations, documentation, code, slides,…
Connect at the Social Mixer with your fellow Bootcampers, meet in person the most renown quants in the industry (Bob Litterman, Peter Carr, Emanuel Derman,..) and stay in touch via the Virtual Classroom and our technical Q&A Forum
Certificate of Completion, 40 GARP CPD, academic credits (partner universities) issued upon successful completion.
MathFinance members get Affiliate Discount:
select ‘Bootcamp onsite’ or ‘Bootcamp online’ > Affiliates > MathFinance
