Editorial
Revga and Bufga
The recent FX options market slang I learned is Revga and Bufga. This is not a joke. Generally, Greeks such as Delta, Gamma, Theta, Rho and Vega are quite common in trading and risk management systems. It is all about the “what-if”: what happens to the price if the spot goes down, or the volatility goes up or the domestic interest rate goes up? For example, Vega is the first derivative of a derivative contract (an option) value with respect to volatility. The mathematical derivative quantifies how much the option’s value would change if the input parameter volatility changed. For practical purposes, one commonly agrees on Vega showing the change caused by a 1% move in the volatility in the actual total value of the contract.
Example: Consider a 6-months EUR call USD put on 1 M EUR ATM (strike 1.3038, market data: spot ref EUR-USD 1.3000, EUR -0.066%, USD 0.247%, FWD 1.30204, ATM vol 7.40%, RR 0.95% in favor of EUR puts, BF 0.25%). To calculate the offer price, we use 7.50% volatility and arrive at EUR 20,300. Vega is 2,800 EUR, and consequently, if volatility rises to 8.50% offer, the option price will be EUR 23,100. Note that the mathematical Vega in the sense of a pure derivative of the Black-Scholes formula with respect to volatility is 0.3633. (Homework question: how does this relate to a Vega of EUR 2,800 that a trading system shows?) There are some conventions to agree on, including the volatility difference, which we have taken to be 1%, and whether one uses a rise or fall or a symmetric change of volatility. And obviously (for the Newton fans) this captures only the linear part of the impact of changing volatility.
Now, we all know that a single volatility is no sufficient for valuation of vanilla options, but rather a volatility surface is required, which captures both smile and term structure. Therefore, when we want to quantify the impact of the change of the volatility surface on the value of the derivative contract, one common way is to use the key input values for the construction of the volatility surface. In FX markets, these are Risk Reversals (RR) capturing the skew, and Butterflies (BF) capturing the convexity of the smile for a fixed maturity. Both RR and BF are liquidly traded standard hedge instruments whose prices are quoted in the brokers’ market. Therefore, it is reasonable to calculate the change of the derivative contract with respect to changes of the key inputs: Vega or Aega represents the change caused by a change in the ATM volatility (level), Revga represents the change caused by a change in the Risk Reversal, and Bufga represents the change caused by a change of Butterflies. Sega refers to the price change caused by a change in the Strangle. There may be another fan club using the term Bega or Butterflega instead of Bufga. In this sense, these “Greeks” are what we call market Greeks, as they translate mathematical derivatives to tradable instruments to hedge the volatility exposure. None of these “Greeks” are actually Greek letters. Even Vega is not a Greek letter, but we needed to have a Greek-sounding alphabet that starts with a “V”.
For the ATM option above, Aega turns out to be identical to the Vega in the Black-Scholes model. Revga and Bufga turn out to be zero, so rather boring. This is because the option is ATM, whence the smile will have no impact on the value as long as the ATM-volatility stays the same. The smile impact will come in when we consider an exotic option: let’s make it a reverse-knock-out (RKO) with barrier 1.4000. The offer price may then be EUR 10,425. A change of the Risk Reversal from -0.95% to +0.05% would lower the offer price to EUR 8,766; therefore Revga is EUR – 1,659. Similarly, raising the Butterfly from 0.25% to 1.25% would lower the offer price by EUR 851 to EUR 9,574, whence Bufga is EUR -851. Note that these figures here depend on the model we use to price the RKO. Depending on your model choice, you may see slightly different figures.
Here is a job for the weekend: how can we approximate Revga for a 25-Delta Risk Reversal? Assuming zero interest rates, the rule of thumb is about 32 basis points of the EUR notional multiplied by the square root of time to maturity, e.g. for a half year Risk Reversal, about 22 basis points (71% of 32). Hence knowing the Revga of any derivative contract, a trader can quickly determine by the rule of three how many Risk Reversals are required for hedging.
To determine the relation between the traditional model Greeks such as Vanna and Volga and the market Greeks, we take Vanna as an example. We illustrate its relationship to Revga for a plain vanilla call in Figure 1. Revga assumes an absolute change of Risk Reversal by 1%. The figure shows that both Greeks are related to the skew, which is why both are zero near the ATM strike. The skew sensitivity for Vanna peaks at the 15-Delta strikes: formally, one can derive the maximum and minimum Vanna to be![]() which is roughly equal to 15% for our 6M call on a volatility of 10%; thus Vega being square root of T multiplied by the normal density at its normal quantile is about 16 basis points, explaining the ratio of 1600 in the figure.
which is roughly equal to 15% for our 6M call on a volatility of 10%; thus Vega being square root of T multiplied by the normal density at its normal quantile is about 16 basis points, explaining the ratio of 1600 in the figure.
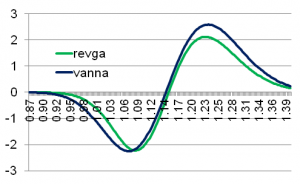
Figure 1: Revga and 1600 Vanna of a 6M vanilla call on the strike space (x-axis) on a 1.1500 spot, zero interest rates, 10% ATM volatility, 0% Risk Reversal, 0% Butterfly
So what is the difference then? Vanna and Volga do not take the smile information into account at all; they are just simply second order model Greeks. Revga and Bufga are market Greeks describing the direct link to market variables Risk Reversal and Butterfly and are therefore extendible to exotics. The reason why they look similar in the graph is that a vanilla option is most sensitive to Risk Reversal changes near the point where Vanna peaks, and with a suitable scaling factor one might think they are generally roughly the same.
Uwe Wystup
Managing Director of MathFinance
____________________________________________
Upcoming Events
FX EXOTIC OPTIONS IN FRANKFURT 2018
December 10 – 12, 2018
Lecturer: Prof. Dr. Uwe Wystup
This advanced practical three-day course covers the pricing, hedging and application of FX exotics for use in trading, risk management, financial engineering and structured products.
FX exotics are becoming increasingly commonplace in today’s capital markets. The objective of this workshop is to develop a solid understanding of the current exotic currency derivatives used in international treasury management. This will give participants the mathematical and practical background necessary to deal with all the products on the market.
Learn more about the training or register directly.
D-FINE DAY WEST: EINBLICK IN DIE FACHLICHE UND TECHNOLOGISCHE BERATUNGSPRAXIS
Quantitative Methoden und komplexe Technologien sind heutzutage fester Bestandteil praxisorientierter Problemlösungen in der Wirtschaft. Beispiele hierzu sind die Bearbeitung von Problemen rund um die Elektromobilität, die Verwendung von KI-Algorithmen zur Betrugsprävention in der Finanzwelt, die Optimierung von Energienetzen, die Verwendung von statistischen Verfahren bei der fortschreitenden Digitalisierung des Health Care Bereichs oder die Optimierung von Frühwarnsystemen im Risikomanagement durch die Verwendung von Machine Learning Methoden.
Möchten Sie von unseren Experten an Hand von Projektbeispielen einen Einblick in diese besondere Arbeitswelt bekommen und den Wandel mitgestalten? Dann sollten Sie d-fine näher kennenlernen. Denn mit solchen Themen und vielen weiteren spannenden und anspruchsvollen Fragestellungen beschäftigen sich unsere Berater. Und sie beantworten die an sie gestellten Fragen durch die Kombination von Methoden, Modellen und Konzepten aus Ökonomie, Mathematik, Physik und Informatik.
Es gibt noch viel Platz für neue Denkansätze und unkonventionelle Ideen bei d-fine. Registrieren Sie sich auf unserer Homepage bis zum 8. Juli 2018. Je früher, desto besser, denn die Teilnehmerzahl ist begrenzt. Wenn Sie also gerade dabei sind, Ihre akademische Karriere mit einem exzellenten Abschluss (BSc, MSc, Diplom oder Promotion) zu krönen und bereit sind, einen Schritt über die Grenzen zwischen akademischer Theorie und Unternehmenspraxis zu gehen, dann sind wir gespannt auf Sie.
d-fine ist ein führendes europäisches Beratungsunternehmen mit Standorten in Berlin, Düsseldorf, Frankfurt, London, München, Wien und Zürich. Mit über 700 hochqualifizierten, naturwissenschaftlich geprägten Beratern unterstützen wir unsere Kunden aus Industrie, Finanzwelt oder öffentlicher Hand bei anspruchsvollen quantitativen, prozessualen und technologischen Herausforderungen. Strategieberatung, Fachberatung, Technologieberatung: d-fine ist alles in einem.
d-fine. analytisch. technologisch. quantitativ.
Halbtägiger Workshop mit Vorträgen sowie Erfahrungsberichten aus der fachlichen und technologischen Beratungspraxis. Bewerbungsschluss ist der 8. Juli 2018.
Termin: Donnerstag, 12. Juli 2018
Ort: Meliá Düsseldorf, Inselstraße 2, 40479 Düsseldorf
Kontakt:
d-fine GmbH
Svenja Dröll
An der Hauptwache 7
60313 Frankfurt am Main
T +49 69 907 37- 555
______________________________________________________________________________________________________
Careers
MathFinance Openings
Senior Quant/ Consultant
We are looking for senior quant / consultant in the areas of
Insurance
- Actuary with 5 to 7 years of experience in insurance or re-insurance
- Experience in quantitative Risk Management in relation to regulatory issues (Solvency II)
- Experience in Capital Management
Banking
- Quant with 5 to 7 years of experience in Banking, ideally in Trading
- Experience in quantitative Risk Management in relation to regulatory issues (Basel III)
- Experience in Capital Management
Investment
- Quant with 5 to 7 years of experience in Asset Management (Funds, Insurance and Family Offices), ideally with emphasis on Risk Management
- Experience in quantitative Risk Management in relation to regulatory issues (German KAGB and KARBV)
Please send us your CV to recruitments@mathfinance.com
Junior Quant
Do the following apply to you?
- Master degree or diploma in (business) mathematics or physics
- PhD or CFA is a bonus
- First experiences in mathematical finance is desirable
- Very good programming skills, e.g. C++, Python or Matlab
- Good language skills in German and English
- Outstanding analytical skills and a problem-solving attitude
- High motivation to develop your knowledge and skills
- Good communication skills and team spirit
Then we would like to hear from you. Please send us your CV to recruitments@mathfinance.com
