Can Vega of a Double-No-Touch be Positive?
While teaching classes on FX exotics over the last 20 years, there isn’t one day I don’t learn something new. In today’s example I would like to share one of the things I learned about the vega of a double-no-touch (DNT).
The DNT pays a fixed amount of currency at maturity if the FX spot trades inside are pre-specified range between inception of the trade and maturity. The range is often chosen symmetrically around initial spot. Buying a DNT will generate a short vega position, which means that if volatility goes up, then the value of the DNT goes down. This is quite intuitive: if volatility goes up, then the probability of the spot hitting any of the two barriers increases; therefore, the chance of getting a payment will be lower. This intuition is very easy to follow, isn’t it? So when I ask if vega of a DNT can be positive, then one of the common answers I get is that it can be if I go short a DNT. This is obviously not what I had in mind.
When we look at the vega profile of a (long) DNT, we easily verify by visual inspection that it is indeed negative. Whether it has two minima or just one depends on the variance, i.e. the product of volatility squared times the remaining time to go. Furthermore, vega must be zero on the barriers, which is where the value of the DNT is zero and terminates once the spot hits any of the barriers. In the example I consider a 1-year DNT in EUR/USD with range 1.0000 to 1.2000 and an initial spot of 1.1200.
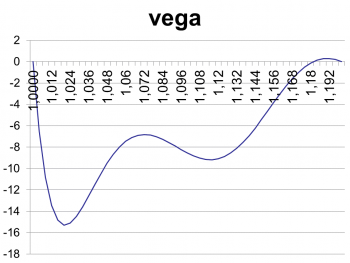
Looking at the chart carefully, we spot a slightly positive vega near the 1.2000 barrier. When I first spotted this, I found it quite disturbing, and initially I thought it must be one of these features of the new Excel version. But, after zooming in to the range 1.1800 to 1.2000, I realized that vega did indeed appear positive.
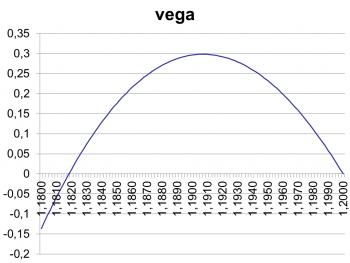
I double checked my code, verified the formula with finite differences and could not find a mistake. So what was going on?
Taking a USD interest rate of 5% and EUR interest rate of 1.5%, we generate a forward curve moving strongly up, so starting from 1.1900, the forward rate reaches the barrier 1.2000 in one quarter. Hence, just looking at the forward curve, we can be sure the DNT will terminate early. This would happen if we didn’t have volatility and the spot would just follow the forward curve. Consequently, with a very low volatility (4% in my example), the spot will stick to the forward curve very closely and lead to an almost sure early termination of the DNT and therefore a zero payoff. Then increasing the volatility will effectively increase the probability of the spot staying away from the upper barrier, in which case the vega is positive for this zone.
And surely, you must have known this feature for a long time☺
Professor Dr. Uwe Wystup, Managing Director of MathFinance AG
UPCOMING EVENTS
D-FINE DAY OCTOBER 2016
D-FINE DAY MÜNCHEN
EINBLICK IN DIE RISIKOMANAGEMENTBERATUNGSPRAXIS
Die Dynamik der Finanzwelt ist ungebrochen: Unsicherheit an den globalen Finanzmärkten durch Treiber wie anhaltende Euro-Krise, Turbulenzen am Rohölmarkt und negative Zinsen stellt Geschäftsstrategien
und Risikomodellierung vor eine schwere Prüfung. Eine Flut neuer Regularien verändert die Rahmenbedingungen, und neue Technologien verändern unseren Umgang mit Geld maßgeblich. Wollen Sie verstehen, was sich dahinter verbirgt und vielleicht den Wandel mitgestalten? Dann sollten Sie d-fine näher kennenlernen. Denn mit solchen Themen und vielen weiteren spannenden und anspruchsvollen Fragestellungen beschäftigen sich unsere Consultants (m/w). Und sie beantworten die an sie gestellten Fragen durch die Kombination von Methoden und Modellen aus Ökonomie, Mathematik und Physik.
Wissenschaft und Unternehmen, alles ist ständig in Bewegung. Es gibt noch viel Platz für neue Denkansätze und unkonventionelle Ideen bei d-fine.
Registrieren Sie sich auf unserer Homepage bis zum 10. Oktober 2016. Je früher desto besser, denn die Teilnehmerzahl ist begrenzt.
Wenn Sie also gerade dabei sind, Ihre akademische Karriere mit einem exzellenten Abschluss (MSc, Diplom oder Promotion) zu krönen und bereit sind, einen Schritt über die Grenzen zwischen Naturwissenschaft und Unternehmenspraxis zu gehen, dann sind wir gespannt auf Sie.
dfine ist mit über 600 Beratern und Büros in Frankfurt, München, London, Zürich und Wien eines der größten auf Projekte rund um die Themen Risikomanagement und Finanzsteuerung spezialisierten Beratungsunternehmen in Europa.
d-fine. Die Spezialisten für Risk&Finance.
½-tägiger Workshop mit finanzmathematischen Vorträgen zum Themenkomplex Kontrahentenrisiko und Erfahrungsberichten aus unserer Consulting-Praxis. Bewerbungsschluss ist der 10. Oktober 2016.
Montag, 24. Oktober 2016
Eurostars Grand Central Hotel
Arnulfstraße 35
80636 München
d-fine GmbH
Svenja Dröll
An der Hauptwache 7
60313 Frankfurt am Main
T +49 69 907 37-555
www.d-fine.de
Frankfurt, München, London, Zürich, Wien
CAREER
MATHFINANCE OPENINGS
MathFinance OpeningsSenior Quant/ Consultant
We are looking for senior quant/ consultant in the areas of
Insurance
- Actuary with 5 to 7 years of experience in insurance or re-insurance
- Experience in quantitative Risk Management in relation to regulatory issues (Solvency II)
- Experience in Capital Management
Banking
- Quant with 5 to 7 years of experience in Banking, ideally in Trading
- Experience in quantitative Risk Management in relation to regulatory issues (Basel III)
- Experience in Capital Management
Investment
- Quant with 5 to 7 years of experience in Asset Management (Funds, Insurance and Family Offices), ideally with emphasis on Risk Management
- Experience in quantitative Risk Management in relation to regulatory issues (German KAGB and KARBV)
Please send us your CV to recruitments@mathfinance.com
__________________________________________________________
Junior Quant
Do the following apply to you?
- Master degree or diploma in (business) mathematics or physics
- PhD or CFA is a bonus
- First experiences in mathematical finance is desirable
- Very good programming skills, e.g. C++, Python or Matlab
- Good language skills in German and English
- Outstanding analytical skills and a problem-solving attitude
- High motivation to develop your knowledge and skills
- Good communication skills and team spirit
Then we would like to hear from you. Please send us your CV to recruitments@mathfinance.com
_________________________________________________________
