Editorial
Static Replication of a FOR-paying Double-No-Touch with One Double-Knock-Out Option
How can we statically replicate a double-no-touch contract (DNT) paying one unit of foreign currency using just one double-knock-out option?
Let the barriers be L and H for the lower and higher barrier respectively. Let the currency pair be FOR/DOM, e.g. GBP/USD. We recall that we can replicate a DNT(L,H) paying one unit of domestic currency can be replicated by 1/(H-L) long call options with strike at L and H-L long put options with strike at H. The notional is in foreign currency (FOR). The difference H-L represents the maximum intrinsic value of the double-knock-out options (DKO), and therefore, the DKO notional needs be the reciprocal of this maximum intrinsic value to generate payoff of exactly one unit of domestic currency.
For the DNT(L,H) paying one unit of foreign currency, the replication is a bit more complicated. Here, we need in fact a DKO put option with strike H and notional L/(H-L) FOR, and a DKO call option with strike L and notional H/(H-L) EUR, which can be derived from the previous result inverting all the currency pairs from S=FOR/DOM to 1/S=DOM/FOR, and inverting all the strikes and barrier levels.
At some point, it struck me, in one of my classes on FX structured products, that one can replicate the FOR-paying DNT(L,H) also with simply one DKO call option. The secret lies in my favorite question: which currency? A payoff in one unit of foreign currency is in fact equivalent to a payoff of S units of domestic currency, where S denotes the final spot price. We omit settlement risk at maturity for this discussion. Then a payoff of 1 with FOR on the y-axis, is equivalent to a payoff of S with DOM on the y-axis, as illustrated in Figure 1.
This is the key insight, as now a payoff of S units of domestic currency can be viewed as a payoff of S-0, i.e. a zero-strike call option payoff. Consequently, the FOR-paying DNT contract is in fact nothing but a zero-strike DKO call option. The fact that the strike is outside the range L to H is possibly unusual, but not critical.
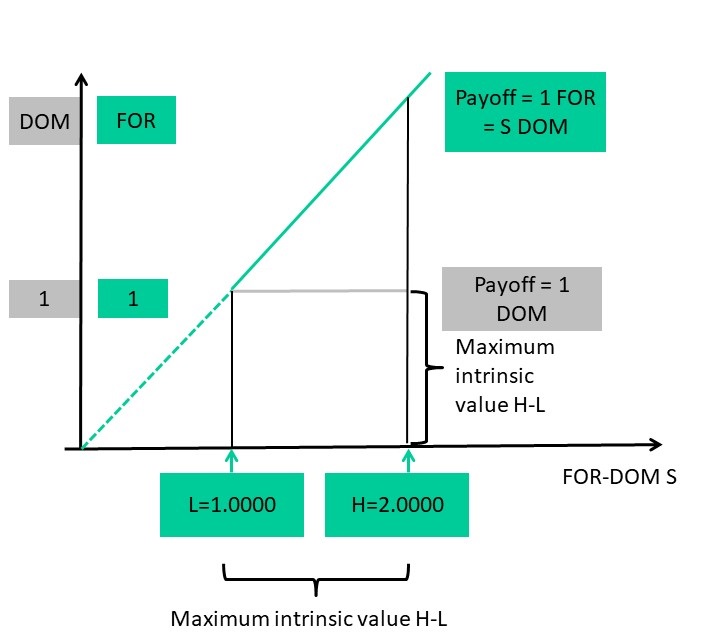
Figure 1: Double-No-Touch Payoff in DOM and FOR Currency
We can use this to perform a sanity check or validation of our pricing library, as both products are in fact identical, they should yield the same value and bid-offer spread in all models. Let us challenge the systems: I get an interesting result in Eikon, illustrated in Figure 2. We price a DNT with L=1.2000, H=1.3000 on a spot reference of 1.2500 with 6M maturity and 1M GBP notional. The hitting probability is quite large, thus the value quite small. As it appears, the system allows arbitrage, as I could buy the DNT for USD 11,450 and sell the DKO for USD 57,701 – in the Black-Scholes model. In the vanna-volga model, unfortunately, even the bid price of the DNT exceeds the offer price. Time for a state-inspection.
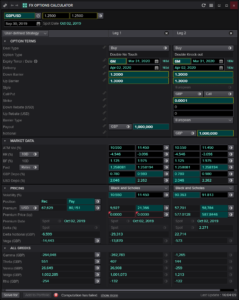
Figure 2: GBP-USD DNT and Zero-Strike DKO Compared in Eikon
Trying something similar in SuperDerivatives, we see in Figure 3 that prices and spreads are quite different in all models. Interestingly, delta seems to be the same for both products, so using delta as a checksum, we can argue that we probably price the same product with two different names. But even here, it is time for an overall engine overhaul.
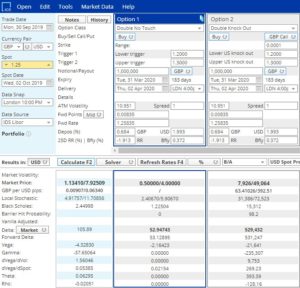
Figure 3: GBP-USD DNT and Zero-Strike DKO Compared in SuperDerivatives
Overall, I can’t stress the relevance of static replication for exotics valuation enough. It is a good tool to apply for vetting pricing libraries and validate models.
Uwe Wystup
Managing Director of MathFinance
Upcoming Events
FX Exotic Options in Frankfurt 2019
December 16 – 18, 2019
Register today for early bird discount!!
Lecturer: Prof. Dr. Uwe Wystup
This advanced practical three-day course covers the pricing, hedging and application of FX exotics for use in trading, risk management, financial engineering and structured products.
FX exotics are becoming increasingly commonplace in today’s capital markets. The objective of this workshop is to develop a solid understanding of the current exotic currency derivatives used in international treasury management. This will give participants the mathematical and practical background necessary to deal with all the products on the market.
Check the details
Register either directly here or use the single registration pdf or the group registration pdf
MathFinance Asia Conference
18th October 2019
Fullerton Hotel, Singapore
Register today for early bird discount!!
The first MathFinance Asia conference aims to bridge the world of quantitative finance and academics. MathFinance organizes its flagship conference in Frankfurt every year and this inaugural conference aims to bring the Asian quantitative finance community together.
The conference is intended for practitioners in the areas of trading, quantitative or derivative research, risk and asset management, insurance as well as for academics studying or researching in the field of financial mathematics.
The half-day event will feature:
2 Panel discussions on FX Derivatives pricing models in Asia, platforms and insights and Latest trends in the FX Options markets in Asia distribution/ pricing for best execution
This event is a must for everyone in the quantitative financial industry.
