Editorial
MathFinance Conference Recap
The 18thMathFinance Conference held on 16-17 April 2018 was once more the key event in Germany for quants. With more than 110 registered participants, visitors from 30 countries attended this two day event in Frankfurt.
In a market that is dominated by increased radical uncertainty, saturated equity markets, low interest rates persistent in EUR/CHF/JPY, and banks in Europe being pushed into avoiding business as much as possible and focus on writing compliance papers by regulators, there are still many areas quants work in, in fact, quantitative modeling is likely to be even more in demand. We included presentations on machine learning and ratings of structured products.
Some of the key abbreviations and phrases in circulation were:
Samuelson effect, Oosterlee scheme, RBM, Sato process, exposure concentration, Haar wavelets, uninformed uniform, CCCP, default waterfall, SLV, LSV, internalization, mixing factor, radial basis functions, supervised learning, SIMM and BIM, toxicity ration, SSR, GETS, cross currency betting arbitrage, swing, Trolle&Schwartz, Moore-Pensore pseudo-inverse.
Let me recap what I learned:
The first morning Karel in’t Hout organized a symposium on Computational Finance selecting key innovations from practice and academia.
- Klaus Spanderen illustrated in his talk on Applications of the Heston Stochastic Local Volatility Model in Commodity Markets, that there is a natural Interest in trading complex contracts at Uniper, which is why they require stochastic-local volatility (SLV) Their main product of interest is the swing contract, which is often requested by their customers as a hedging instrument. While traditionally traders think in terms of a model-free replication, quants have implemented a Heston-based SLV model in a PDE framework, in which they always get the right price, and which is more robust, compared to Monte Carlo, where one gets only lower bounds combined with simulation errors. To model the Samuelson effect–volatility of forward contracts shoots up as time to maturity decreases – the SLV model works with a local factor only in time, but less focus on the skew. It was refreshing to see that for the Heston calibration the Lewis formula is back. For the spot simulation, Spanderen pointed to the Oosterle scheme (2013), which is an extension of Andersen’s quadratic exponential scheme with volatility freezing.
- Silke Glas motivated her talk about Model Reduction Techniques for Financeby the increased need to perform complex calculations in less time. Her reduced basis method (RBM) leads to a split into an offline part to prepare and an online part. Applications can be found in commodity markets. Glas also extends RBM to non-linear models. A proximity indicator helps determine if a solution exists.
- Lynn Boen spoke about Building and Calibrating Multivariate Sato Models with Linear Dependence. Based on the well-known shortcomings of Lévy processes including (a) the moment term structure being opposite to market observations and (b) the reproducing of volatility surfaces being difficult, Boen proposed Sato processes, which can be constructed from any self-decomposable random variable, with intended time-inhomogeneous increments. The application to keep in mind is multivariate option pricing. An example is a variance gamma process as a building block, which can be decoupled for calibration. Boen compared the decoupled calibration with a joint calibration and showed in an example that correlation fitting can be improved by joint calibration, in order to achieve a much better fit of the dependence structure.
- Luis Ortiz-Gracia Quantified Credit Portfolio Losses under Multi-Factor Models. He investigated numerical methods to obtain VaR and ES values for portfolios with exposure concentration under multi-factor Gaussian and t-copula models. They are composed of two main parts: (a) the numerical computation of the characteristic function (CF) of the loss variable and (b) the Fourier inversion method based on the Haar wavelets to recover the CDF of the loss variable. This research opens the door to calculate the risk contributions to the VaR and ES risk measures under the same model assumptions.
- Andreas Fontanari impressed with his Modeling of Joint Mortality and its Impact on Annuity Contracts. One of the most critical methodologies includes the estimation of the survival function, as Solvency II regulations requires that “the best estimate shall correspond to the probability-weighted average of future cash-flows.” Fontanri’s solution is a Baysian non-parametric general setup. We will probably all remember the uninformed uniform as a prior distribution. Even here, the posterior shows reasonable results as illustrated in the graph below.
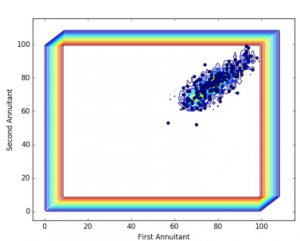
The conference proceeded with more highlights:
Tomasz Bielecki presented his Dynamic Model of Central Counterparty Risk. Following the aftermath of the financial crisis of 2008, starting with the 2009 G-20clearing mandate, regulators across the globe are required that standardized OverThe Counter (OTC) derivative contracts are cleared by Central Clearing Parties (CCPs). Bielecki entertained us all by explaining that actually Central Counterparty Clearing Parties would have to be abbreviated by CCCP. His main goal is to develop a new methodology for computing some of the CCP’s default waterfall in a dynamic framework.
In his talk about Corridor Variance Swap Spreads Bryan Jianfeng Liang motivated his approach by market participants performing relative value volatility trades: they buy variance of an index with low premium (such as Asian or European indices) and sell variance of an index with a high premium, typically SPX. Liang explains that a single-asset corridor variance swap can be replicated by vanilla options with strikes within the corridor at the final maturity, a continuous stream of vanilla options of intermediate maturities, and a dynamic portfolio in the underlying S. This reminded me of the semi-static hedge of reverse-knock-out barrier options with vanilla option portfolios. In the sequence Liang compares various multi-factor models for the two-asset case. One key result is that LV+LV is unable to capture the vol-of-vol risk, cross spot/vol correlation risk.
Peter Hahn took us through The Global FX Market. This largest of all financial markets is going to be more dominated by the Chinese Yuan and by the best platforms and technology.Most stunning was his illustration that cables are again used for information arbitrage just to be 5 milliseconds ahead. As in Roel Oomens talk of last year, the success of the FX spot trading business will be dominated by the extent the provider can internalize the trades.
Christoph Reisinger talked about Efficient Exposure Computation by Risk Factor Decomposition. On the portfolio level, the large number of risk factors rules out traditional PDE-based techniques and allows only a relatively small number of paths for nested Monte Carlo simulations, resulting in large variances of estimators in practice. Reisinger proposed a novel approach based on Kolmogorov forward and backward PDEs, where he counters the high dimensionality by a generalization of anchored-ANOVA decompositions. He attains effective dimension reduction in model problems, versatility through control variate MC and an easy couplingwith other accelerations, parallelization, QMC etc. A test in production situation is the logical next step.
William McGhee gave an overview of Machine Learning in Quantitative Finance, which included
- History of Machine Learning: from MENACE to Alpha Go Zero
- Machine Learning Algorithms
- The changing role of Quants
- Applications within Quantitative Finance
- Practical considerations: from technology to governance.
Jürgen Hakala applied Machine Learning to SLV Calibration: He takes us from kernel estimation via Regression to calibration as supervised learning. Radial Basis Functions (RBF) – compare with RBM in Glas’ talk above – are quite close to kernel regression as the functions used are of the same type. But it reduces the computational burden by taking a small number of kernels compared to the number of examples. As one of the highlights Hakala presented the estimation of the mixing factor in EUR/USD, which turns out to be 66% for 6 months maturity using the one-touch contract as exotic input for the SLV calibration, which is very close to a result found by Murex as commented from the audience.
Adil Reghai continued the LSV saga by Fair Pricing in the Presence of Local Stochastic Volatility, taking us back the cost of the hedge. He motivates the need by pricing the most actively traded instrument in the equity derivatives space, i.e. the auto-callable. Again, it is about finding the right level of fine-tuning the mixing parameter in order to price and hedgeit in a consistent way. It starts with linking a dynamic property of the market Skew Stickiness Ratio (SSR) with its equivalent mixing weight to pick the right model out of a group of models. His result for the mixing weight on EUR/USD of 65% is in fact close to Hakala’s finding of 66%. Absolutely Amazing, but it’s been the second day of the conference. Reghai furthermore introduces the concept of a toxicity ratio, zero permitting a replication by vanilla options, and one being a very toxic product. With this index he concludes with a proxy formula to calculate the price of an exotic product, both in the single-asset and the multi-asset case.
A completely new aspect to the conference was brought in by Bereshad Nonas, Simulating Hedge Fund Strategies – Generalizing Fund Performance. The challenges include that (a) hedge funds are idiosyncratic by construction, (b) there is – if at all – only a short time series of a fund’s performance, and (c) the complex dependence structure. Nonas reduces the modeling effort with general-to-specific model selection (GETS) and maps hedge funds to indices, generalized hedge funds to hedge fund strategies. He concludes with good out-of sample test results, but clearly points out that everything depends on data quality.
Applications of Machine Learning for Volatility Trading and Asset Allocation were explained by Artur Sepp: Most applications of quantitative trading and investing require the forecast of the future realized volatility as a key input. While there are many models for volatility measurement and forecast, the key decision is how to select the best models with the highest predicative power for a given application. Sepp applied the methods of supervised machine learning and hence ranked for the machine-based selection of volatility models. He demonstrated applications of this framework to trading strategies in implied vs. realized volatilities, to designing volatility-targeting products, and to implementing risk-based and risk-parity allocations. In particular, he pointed out that machine learning can be applied for automated risk management of options books.
Rolf Poulsen was back with one of his stunning findings, this time How Accurately did Markets Predict the GBP/USD Exchange Rate around the Brexit Referendum. Now, obviously, markets aren’t able to predict the outcome. However, both in the GBP/USD case as well as in the USD/MXN case of December 2016 the financial markets were stunningly accurate in their expectations conditional on the election outcome. The market/the model is able to separate views on the likelihood and on the impact of election outcomes. (Try doing that in a credit/liquidity risk model.) Poulsen made us aware that in view of cross currency betting arbitrage there really should be geographical differences in the odds.
Karl Hofmann and Patrick Büchel presented an HJM-Type Stochastic Spread Model – Theory and Implementation. This has been motivated by:
- LIBOR-OIS spread cannot be neglected since 2007, with very low magnitudes before 2007;
- Market standard in valuation and XVA calculation is recognition of LIBOR-OIS spread in a deterministic manner;
- Considerable movement in LIBOR-OIS spread can be observed, but is typically not modeled stochastically in valuation context.
In the interest rates the practical implementation included
- Multi curve setting (extension to stochastic bases (tenor bases (TB) & CCY bases))
- Affine term structure model with stochastic volatility to model smile and skew (Trolle & Schwartz, a stochastic volatility Cheyette Model, calibrated to European swaptions)
The various impacts on FVA were discussed.
Christian Kappen approximated MVA along Low-Dimensional State Spaces. ISDA’s Standard Initial Margin Method (SIMM) includes the Bilateral Initial Margin (BIM), whichis collateral which is meant to mitigate, at the 99% quantile level, the counterparty credit gap risk that is generated by market induced portfolio price movements over a 10 day horizon. Kappen comes to several conclusions:
- Computing the initial margin amount in a simulated future scenarioat a reasonable level of accuracy does not require the computation of the vector of all future market sensitivities in that scenario.
- Instead, it suffices to compute a small number of model sensitivities and the model-to-market Jacobian: initial margin can be recovered from the model sensitivity vector via the Moore-Penrose pseudo-inverseof the model-to-market Jacobian. This technique is what he calls the projection method.
Jessica James concluded the conference on Drivers of the Cross Currency Basis. While there is a noticeable difference between the calculated FX forward rate implied from interest rates and the traded forward price, James explains why trading this doesn’t work after all. Her requirement to model it is in line with Hofmann and Büchel’s presentation, particularly with regards to XVA calculations. Basis swaps can’t be arbitraged for multiple reasons including capital cost of FX derivatives, counterparty risk and credit limits, as well as clearing. At the end of the day we all wished we knew more.
Overall, I learned a lot from all the speakers. I would like to thank all the speakers and sponsors to help make this conference the key content-driven event for quants. It turns out that we quants have a really good business model: first we point out the complexity of the markets and the need to model underlying and volatility as stochastic, model dependence structures in the very detail, included credit, liquidity, longevity and what have you; and when everything is implemented and calibrated we suggest ways to reduce complexity by various projection methods. The show must go on.
Watch the conference video at https://youtu.be/20jraV-FqBA
We hope to see you all again at our future events. Save the next conference date: 25-26 March 2019.
Uwe Wystup, Managing Director of MathFinance
Upcoming Events
FX EXOTIC OPTIONS IN FRANKFURT 2018
August 20 – 22, 2018
Lecturer: Prof. Dr. Uwe Wystup
This advanced practical three-day course covers the pricing, hedging and application of FX exotics for use in trading, risk management, financial engineering and structured products.
FX exotics are becoming increasingly commonplace in today’s capital markets. The objective of this workshop is to develop a solid understanding of the current exotic currency derivatives used in international treasury management. This will give participants the mathematical and practical background necessary to deal with all the products on the market.
Learn more about the training or register directly.
D-FINE DINNER FRANKFURT
Sie interessieren sich für einen Einstieg in die fachliche und technologische Beratungspraxis und möchten sich über dieses spannende Berufsfeld informieren? Dann lernen Sie d-fine als Arbeitgeber beim d-fine Dinner in Frankfurt kennen! In persönlicher Atmosphäre können Sie sich mit Mitarbeiterinnen und Mitarbeitern unterschiedlicher Karrierestufen austauschen und haben so die Möglichkeit, unsere Unternehmenskultur kennenzulernen und Ihre individuellen Fragen zu stellen.
d-fine ist ein führendes europäisches Beratungsunternehmen mit Standorten in Berlin, Frankfurt, London, München, Wien und Zürich. Mit über 700 hochqualifizierten, naturwissenschaftlich geprägten Beratern unterstützen wir unsere Kunden aus Industrie, Finanzwelt oder öffentlicher Hand bei anspruchsvollen quantitativen, prozessualen und technologischen Herausforderungen. Strategieberatung, Fachberatung, Technologieberatung: d-fine ist alles in einem.
Bei einem gemeinsamen Abendessen können Sie sich mit den d-fine Kolleginnen und Kollegen zur Projektvielfalt bei d-fine, dem Berufsalltag in der Beratung, Ihren Einstiegsmöglichkeiten – ob Praktikum oder Direkteinstieg – und allen weiteren Themen austauschen. Gerne informieren wir Sie an diesem Abend auch über die unterschiedlichen Einstiegswege bei d-fine, mit Wohnort und Projekteinsätzen ausschließlich im Rhein-Main-Gebiet oder alternativ mit flexiblem Wohnortprinzip innerhalb Deutschlands und überregionalen Projekteinsätzen.
Nutzen Sie die Chance, um einen Einblick in das Beratungsgeschäft bei d-fine zu erhalten und bewerben Sie sich bis zum 3. Juni 2018 mit Ihrem aktuellen Lebenslauf oder dem auf unserer Karriereseite hinterlegten Anmeldeformular.
Ihre Reisekosten für das d-fine Dinner werden bis maximal 100 € gerne von uns übernommen. Nach Rücksprache ist die Übernahme höherer Reisekosten ggf. auch möglich.
Wir freuen uns auf den gemeinsamen und informativen Abend mit Ihnen und stehen Ihnen bei Fragen gerne unter 069 / 90 737 555 oder careers@d-fine.de zur Verfügung.
d-fine. analytisch. technologisch. quantitativ
Termin: Do. 7. Juni 2018 um 18.00 Uhr in Frankfurt / Main (Nähere Informationen zum Veranstaltungsort erhalten Sie mit der Einladung).
Bewerbungsfrist: So., 3. Juni 2018
Zielgruppe: Studierende, Promovierende und Post-Docs der Fachrichtungen Physik, Mathematik, Informatik und Wirtschaftsingenieurwesen
Careers
MathFinance Openings
Senior Quant/ Consultant
We are looking for senior quant / consultant in the areas of
Insurance
- Actuary with 5 to 7 years of experience in insurance or re-insurance
- Experience in quantitative Risk Management in relation to regulatory issues (Solvency II)
- Experience in Capital Management
Banking
- Quant with 5 to 7 years of experience in Banking, ideally in Trading
- Experience in quantitative Risk Management in relation to regulatory issues (Basel III)
- Experience in Capital Management
Investment
- Quant with 5 to 7 years of experience in Asset Management (Funds, Insurance and Family Offices), ideally with emphasis on Risk Management
- Experience in quantitative Risk Management in relation to regulatory issues (German KAGB and KARBV)
Please send us your CV to recruitments@mathfinance.com
Junior Quant
Do the following apply to you?
- Master degree or diploma in (business) mathematics or physics
- PhD or CFA is a bonus
- First experiences in mathematical finance is desirable
- Very good programming skills, e.g. C++, Python or Matlab
- Good language skills in German and English
- Outstanding analytical skills and a problem-solving attitude
- High motivation to develop your knowledge and skills
- Good communication skills and team spirit
Then we would like to hear from you. Please send us your CV to recruitments@mathfinance.com
