The 21st MathFinance Conference on 15-16 March was held online second time and was once more the key event for quants. Many participants from all over the world could join us this year, including Singapore, Malaysia, Australia, Europe, and America. We never had so many participants, almost trice as many as in previous years, because we all didn’t have to travel.
Delegates joined from many banks including DBS, Commerzbank, Danske, Deka, Saxo, Citi, Barclays, Deutsche Bank; large delegation joined from our sponsors Deloitte and VolaDynamics, Also researchers were present from many universities including Antwerp, Imperial College, Frankfurt School, Sperbank Corporate University, and Copenhagen.
When I looked at the final agenda, I notice a strong dominance of 4 Danish speakers.
Let me recap the highlights:
Thorsten Schmidt kicks off with Estimating Risk Measures in the Presence of Heteroscedasticity, where he uses Long-Short-Term Memory (LSTM) as an efficient way to calculate unbiased risk measures. As an example he applies his approach to GARCH models and shows that is outperforms all existing other approaches.
Rama Cont continues with Price Excursions: a Novel Approach to Dynamic Trading Strategies, explaining that in dynamic trading strategies, mostly trades are done based on signals rather than fixed points in time, and that there is a waiting period followed by a holding period. Hence, P&L actually depends on the number of excursions rather than the distribution of the underlying. As a natural consequence, we really need to get hold of the hitting times and then have an easy ride. The realized profit converges to the local time, so local time has a very practical interpretation. He also relates the number of transactions and realized profit to the Hurst exponent / roughness index.
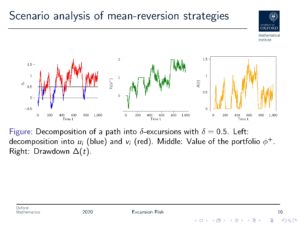
Blanka Horvath presents A Data-Driven Market Simulator for Small Data Environments, picking up Rama’s definitions, and addresses the quantity of training data. There is in fact an increasing demand for synthetically generated training data, but models are not always realistic. In her new concept “Market Generator” she uses market simulations, aiming for something completely non-parametric and model-free.
Rolf Poulsen, who has been regularly attending the MathFinance Conference, shared his Poly Parrot story, a polynomial regression setting to parrot the results of Huge & Savine (2020), presented at our last conference. He conducts a simulation in the Bachelier model, then regresses call option payoffs on powers of the starting values and concludes that a 4th degree polynomial picks up the structure of the call option value quite well.
Mario Dell’Era presents Machine Learning and Option Pricing, applying Neural Networks (NN) to derivatives pricing. He explains convolutional NNs for path recognition and recurrent NNs for time series analysis. For option pricing he designs a feed-forward network called PET-net, an Architectural Neural Network (ANN) with learning rate settings. The ANN solver is typically decomposed into two separate phases, a training phase and a test phase. Errors are measured by MSE or RMSE. Adil comments that his trading team proposed a 95%-quantile in the same approach, rather than aiming for certainty.
Travis Fischer continues with Martingale Modeling for the USD-HKD Exchange Rate. The exchange rates EUR-CHF and USD-HKD require a jump-reflection model for pegged currency markets. He starts with the 1.2000 one-sided peg in EUR-CHF, continued by a de-peg phase. USD-HKD serves as a model with a two-sided peg in the interval 7.75 and 7.85. The central peg 7.80 was held since 1983, by direct intervention of the HKMA. Notable, the forward rate often exceeds the bands, but the spot rate does not.
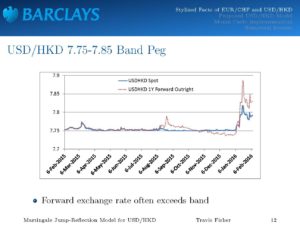
Realized volatility is higher away from the bands, which leads to well-known frown shaped smiles in USD-HKD. After presenting the stylized facts, Travis proposes a jump-reflection model + local volatility, picking up local time. According to the Skorohod Lemma, there is a unique way to modify a process, when it hits a level, to stay above that level. This models a reflection and mimics central bank intervention. Travis concludes with simulating the process using the martingale condition and calibrates the model to vanilla option prices. The resulting prices of one-touch contracts vary hugely compared to SLV models when the barrier is chosen outside the peg band.
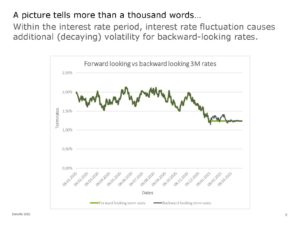
Fabio Mercurio, back to speak at the MathFinance conference, picked up the current challenge IBOR Transition: Looking Forward to Backward-Looking Rates. Moving away from IBOR, the new risk-free rate benchmarks are overnight rates. However, LIBOR is a term rate, so overnight rates need to be converted into term rates. This leads to an extension of the classic single-curve LIBOR Market Model (LMM), which we call generalized Forward Market Model (FMM). This can accommodate both traditional forward looking (LIBOR-like) rates and the new setting-in-arrears backward looking rates. Fabio warns us all that forward rates now have decaying volatility. Overall, we have seen a very intuitive extension to LMM.
Karl Hofmann picks up Fabio’s work in his talk on Implied Volatilities for Options on Backward-Looking Term Rates, providing an overview of the various activities with respect to the new reference rates.
Karl also presents a valuation formula in the Hull-Whit 1-factor model.
In the panel discussion on LIBOR Transition many of the issues were discussed.
Alexandre Antonov started the second day with Black Basket Analytics for Mid-Curves and Spread-Options, first summarizing the drawbacks of copulas, which includes the limited number of parameters and an often painful numerical realization. Alternative multi-dimensional processes like Heston 2D can be considered, but the spread option price is not available analytically. Alexandre uses a basked of log-normal processes, called the Black-Basket, using Black models. With this approach , the Gaussian copula is a special case. We gain high parametric freedom and an analytically tractable model for IR spread options. Congratulations!
Antonis Papapantoleon continued with Deep learning in Finance: an Empirical Investigation. While Deep Learning (DL) and Neural Networks (NN) can be applied to computation of option prices in BS, NIG, as well as computation of implied volatility, the aim is to understand empirically how the different parameters affect these computations, e.g. the number of neurons, number of layers, network architecture, learning rate, activation function, the generated data (Latin Hypercube is back!), reduced training data, full training data, test data. The key result: we need more layers and neurons for a more complex model (surprise, surprise).
Adil comments that a really fast and best way to use DL is to combine analytic formulas with learning
Eric Vynckier added that we need “AI explainable”, as we are potentially better positioned to establish the approach if it can be economically supported.
Oskar Mencer and Erik Vynckier then presented Risk, Cost and Reward of Computing Risk, kicking off with the questions “Do you REALLY need Real Time Risk? How about a real time risk chip?” Traditionally, risk is shown based on the previous day data, but how about a real time risk dashboard? Real time FX risk analytics has been implemented. And actually, risk can be reduced; computation speeds up largely, with a risk library, allowing fast prototyping of dashboards, supporting teams to collaborate. There is a risk chip consortium, developing chips especially for financial engineering, a chip more affordable than the FPGA. A lot of time goes into bootstrapping, discounting, but many computations can be done effectively.
The next highlight was Kwant Daddy Jesper Andreasen’s talk on American Option Pricing in a Tick -Calibration in a Click:
In the equity options market Jesper’s work goes back to his 2006 BOFA working paper “the fastest Bermuda pricer in the West” which in turn uses McKean’s 1965 paper on A free boundary problem for the heat equation arising from a problem in economics. With 1M listed options tradable at Saxo, so about 500 per underlying stock, we face two challenges: computer and man power. The market convention of market makers appears to be binomial trees, still, with constant rates, dividends, and volatilities. Notably the early exercise boundary has two branches when dividend rates exceed interest rates.
Jesper then showed us an integral representation of the American call as sum of a European call plus the early exercise premium, which requires knowing the exercise boundary, though. One then discretize the integral and use a recursion to back out the early exercise boundary; this result goes back to Kim 1990 and allows O(10,000) American options per second. Can we do better? Indeed, using a Fix Point Integral Equation, a vector equation in time works wonders. Also we can use the smooth pasting condition, see Andersen, Lake and Offengenden (2016).
With all this combined he can price O(100,000) American options, so approximately 100 times faster than binomial trees. So” under ruling market conventions it does allow you to calibrate quicker than others can price”.
Josef Teichmann than presented Consistent Recalibration Models and Deep Calibration. Consistent Recalibration models (CRC) have been introduced to capture in necessary generality the dynamic features of term structures of derivatives’ prices. Several approaches have been suggested to tackle this problem, but all of them, including CRC models, suffered from numerical intractabilities mainly due to the presence of complicated drift terms or consistency conditions. He overcomes this problem by machine learning techniques, which allow to store the crucial drift term’s information in neural network type functions. This yields first time dynamic term structure models which can be efficiently simulated.
Natalie Packham performed Copula-Based Hedging of Crypto Currencies and first clarifies this is about hedging crypto spot with futures (not options with the spot). CME is issuing bitcoin futures since 2017 and bitcoin options since 2020, deribit does OTC contracts. Futures are fairly liquid; the underlying is the Bitcoin Reference Rate (BRR, not traded). Now, hedging bitcoin exposure with bitcoin futures means basis risk, with BRR not traded.
In her talk she determines the optimal hedge ratio h for one spot minus h futures. She revisits Sklar’s theorem and examples of copulas. With ratio h=1, many spots don’t appear to be properly hedged with the futures contracts. A box plot shows “far outliers”. Remarkably, most copulas imply hedge ratios h slightly below 1.
Hedging with different copulas and risk measures produces mixed results:
- Frank copula underperforms consistently
- NIG and Gaussian Mix produce small hedge ratios pre-Covid-19 pandemic
- NIG factor produces good hedge effectiveness
- Gumbel produces good results in P&L
Antoine Jack Jacquier was next with Extracting Information from the Implied Volatility Smile Climbing on Roger Lee’s shoulders. Many results are completely model free. The first question is whether it is possible to create a function of T and x that fits data (and does not allow arbitrage). He can now use the resulting extended Lie formula, can now directly derive variance swap formula by direct integration of the smile, but only if you have a continuous (smooth)
Timothy Klassen presented Tools for Option Trading in a Crazy World. Comparing 2008 SPX vs. 2020 smiles shows negative curvature; this had never happened before. New dimensions of craziness have opened up over the last couple of months. Tim still argues it’s best to have a parametric volatility surface, rather than non-parametric ones. Revisit his illustration of negative curvature for the Amazon stock for short maturities exhibited in 2018:
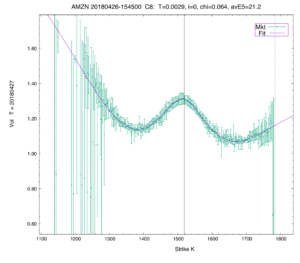
On slide 30 he clarifies what is a “good” volatility curve fit. Tim states and argues that sometimes “The fit is better than the market”. In fact, traders spend hours massaging the volatility surfaces if the fit is not good. Even consensus pricing service does not always match the market, see AMZN on 2020-09-17 T=3m. Another crazy observation is: SPIBOR, i.e. option implied discount factors, does actually not match the rates otherwise observed. So anymore questions on equity volatility surfaces I would safely place with VolaDynamics.
Arun Verma shared with us Quantitative Trading Strategies & Asset Pricing Using Machine Learning.
He explains the use of alternative data in quant trading, the marriage between ML and Finance, and how Bloomberg is learning from news. The idea is picking up sentiments from the market to build a sentiment indicator. It turns out that news can be explained by very few factors. Traditional methods for derivatives pricing can be made efficient via ML. Arun encourages us to think of ML as a way to enhance the quant models, rather than to replace them. For instance, one can use ML for illiquid asset pricing, e.g. when for some bond prices there are no regular updates. ML can help solving for unknown values in a matrix of bond prices.
Jesper Toft added his practitioners’ view in Business Meets Quant, Meets Crypto. In his platform he showed that there can be an alternative to crypto currencies with low volatility, which he calls the Global Stability Unit (GSU). His vision is that this will soon be a currency traded on the market that allows corporates and investors to stay immune to currency fluctuations. In any case, his platform is ready, even on the smart phone. National equilibrium rates can illustrate the pressure on a currency. DKK is about 5% off the EUR peg.
Jesper argues that currency stability can contribute a lot to many countries’ economies. GSU is low vol, and tradable. And furthermore, since all money is FIAT money anyway, GSU might help as a low volatility currency of similar FIAT quality.
Saeed Ameen had the last slot in the conference and presented Developing FX Options Systematic Trading Strategies in Python, where he shared his extensive Backtesting FX options trading strategies.
Overall, I learned a lot from all the speakers. I would like to thank all the speakers, sponsors and media partners to help make this conference the key content-driven event for quants. It turns out that mathematical finance is a core asset of the financial industry. As the most common trends I have seen
- High performance is achievable by the right mix of models, clever math and information technology. Special hardware is available for valuation and risk calculations.
- Combining Neural Networks, Machine Learning with asymptotic formulas makes the approach really fast; however, regulators are still reluctant to accept these for pricing and risk reporting.
- Our panel discussion on LIBOR transition came right in time. It appears there are still a lot of practical points missing, especially for treasury software vendors.
- We don’t have time locally at the moment, but local time has been explained as a relevant concept with practical explanations (realized profit) and relevance in pegged currencies.
Please join the MathFinance Conference group on Linkedin for updates on conference or discussions with other delegates and speakers: https://www.linkedin.com/groups/12181442/
We hope to see you all again at our future events. Save the next conference date: 21-22 March 2022 in Frankfurt – unless of course we have to go digital again.
Uwe Wystup, Managing Director of MathFinance
Upcoming talks and courses:
I am speaking at the 7th Quant Insights Conference on the 27 May 2021.
Title: Mixed Local Volatility Models for FX Derivatives, 9:10 am CEST.
Book your free ticket to join online talks from myself and many more speakers: https://lnkd.in/dxrRmdw

Vanilla FX Options for Professionals – by Prof Uwe Wystup
CEETA 22-23 June 2021 in Warsaw (Interactive live broadcast from CEETA Live studio)
http://ceeta.pl/post/vanilla-fx-options-for-professionals-by-prof-dr-uwe-wystup
FX Exotic Options – by Prof Uwe Wystup
London Finance Studies 19-21 July 2021 in London
https://www.londonfs.com/course/FX-Exotic-Options
————————————————————————————————————————————-
MathFinance Trainings
MathFinance is excited to offer in-house as well as external training courses on the following subjects:
– FX Options & Structured Products
– Machine Learning & Artificial Intelligence Applications for Financial Markets
– Credit Risk Modelling: IFRS 9 & Stress Testing
For further details on our other offerings please visit:
https://www.mathfinance.com/trainings/



![]()



